В трех вершинах квадрата со стороной 20 см расположены положительные заряды по 10^–8 Кл каждый. Какую работу надо совершить, чтобы перенести из четвертой вершины в центр квадрата положительный заряд 1 нКл?

Металлический шар радиусом 5 см, заряженный до потенциала 100 кВ, соединили длинной проволокой с незаряженным металлическим шаром, радиус которого 6 см. Определить заряд каждого шара и их потенциалы. Ответ: 0,25 мкКл, 0,30 мкКл, 45,45 кВ.

Определить поток Фe вектора напряжённости электрического поля через одну из граней куба, если точечный заряд q расположен 1) в центре куба; 2) в одной из вершин куба, не лежащей на данной грани.

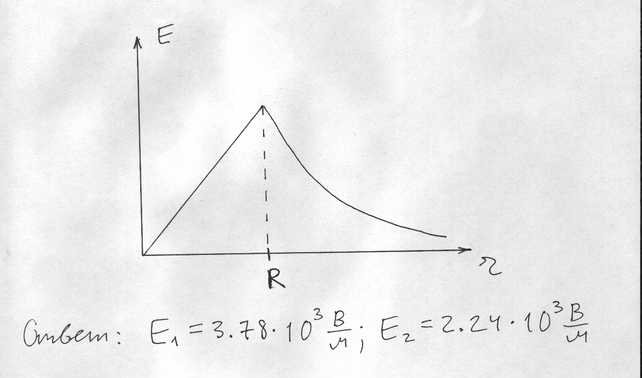
Объёмная плотность заряда равномерно заряженного шара радиусом R = 6 см, изготовленного из диэлектрика с проницаемостью Eш = 2, равна ro=6.7×10-6 Кл/м3. Найти напряжённость E электрического поля на расстоянии r1 = 3 см и r2 = 9 см от центра шара, считая, что относительная диэлектрическая проницаемость среды, в которой находится шар, равна Eср = 3. Построить график зависимости напряжённости поля как функции расстояния от центра шара.

Определить вращающий момент М, действующий на диполь в однородном поле с напряжённостью Е =3×10-4 В/м, если заряды диполя численно равны двум зарядам электрона каждый, а плечо диполя равно l = 5.0×10-9 см. Ось диполя составляет угол alfa= 45град с направлением внешнего поля.

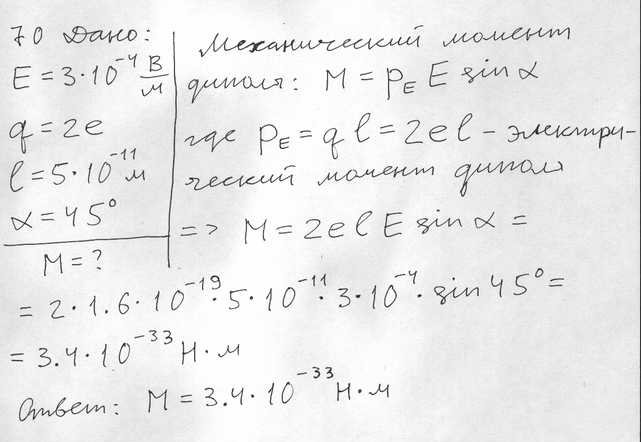
Маленький шарик, несущий заряд 20 нКл, приведен в соприкосновение с внутренней поверхностью полого металлического незаряженного шара радиусом 20 см. Найти поверхностную плотность заряда шара после соприкосновения.