Диск вращается с угловым вращением ε = -2 рад/с2 . Сколько оборотов N сделает диск при изменении частоты вращения от n1 = 240 мин -1 до n2 = 90 мин -1 . Найти время t, в течение которого это произойдет.

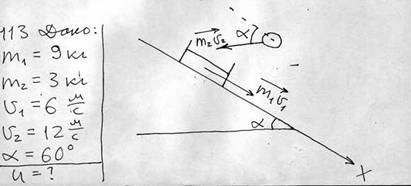
В ящик с песком массой 9 кг, соскальзывающий с гладкой наклонной плоскости, попадает горизонтально летящее ядро массой 3 кг и застревает в нем. Найдите скорость ящика сразу же после попадания ядра, если непосредственно перед попаданием скорость ящика равнялась 6 м/с, а скорость ядра = 12 м/с. Угол наклона к горизонту 60º.

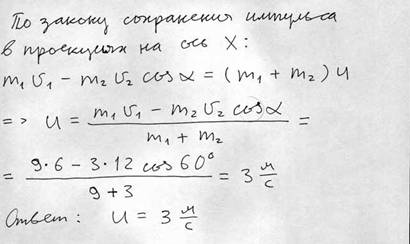
Тело массой m1 = 3 кг, движется со скоростью v1 = 2 м/с и ударяется о неподвижное тело такой же массы. Считая удар центральным и неупругим, определить количество теплоты, выделившееся при ударе.

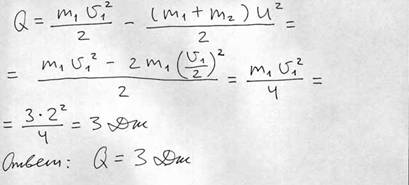
Пружина жесткостью k = 10^4 Н/м сжата с силой F = 200 Н. Определить работу внешней силы, дополнительно сжимающей эту пружину еще на L = 1 см.

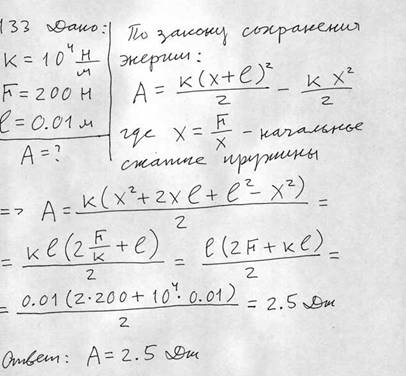
Принимая, что радиус Земли известен, определить на какой высоте h над поверхностью Земли напряженность силы тяготения равна 4,9 Н/кг.

Полый тонкостенный цилиндр массой m = 5 кг, катящийся без скольжения, ударяется о стену и откатывается от нее. Скорость цилиндра до удара о стену v = 1,4 м/с. Определить выделившееся при ударе количество теплоты Q.

Человек массой m = 60 кг, стоящий на краю горизонтальной платформы радиусом R = 1 м и массой M = 120 кг, вращающейся по инерции вокруг неподвижной вертикальной оси с частотой n1 = 10 мин-1 , переходит к ее центру. Считая платформу круглым однородным диском, а человека – точечной массой, определить работу, совершаемую человеком при переходе от края платформы к ее центру.

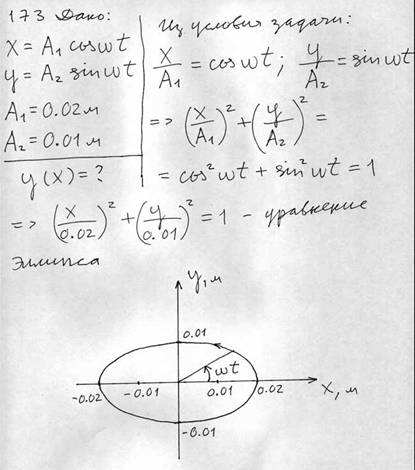
Точка участвует одновременно в двух взаимно перпендикулярных колебаниях, выражаемых уравнением x = A1 cosωt и y= A2 cosωt , где A1 = 2 см, A2 = 1 см. Найти уравнение траектории точки и построить ее, указав направление движения.